Alex Kokot
Ph.D. Candidate in Statistics at the University of Washington.
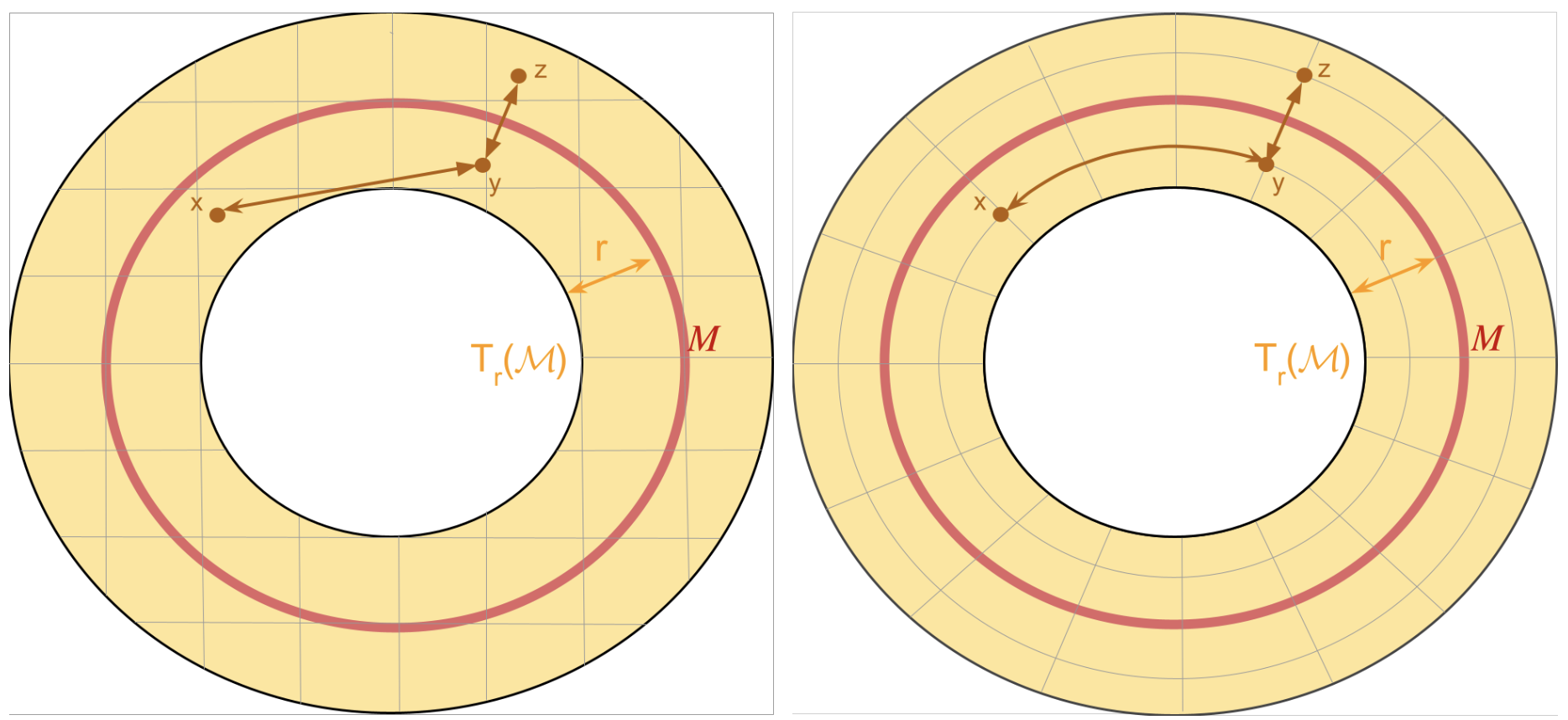
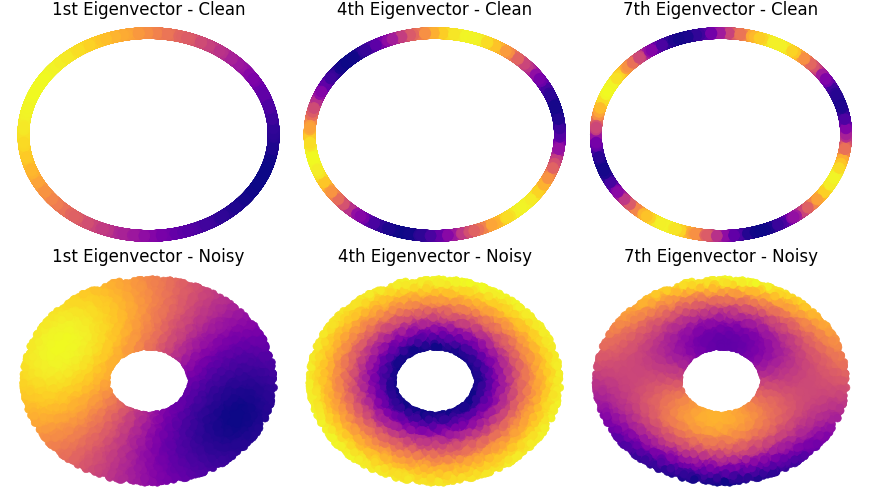
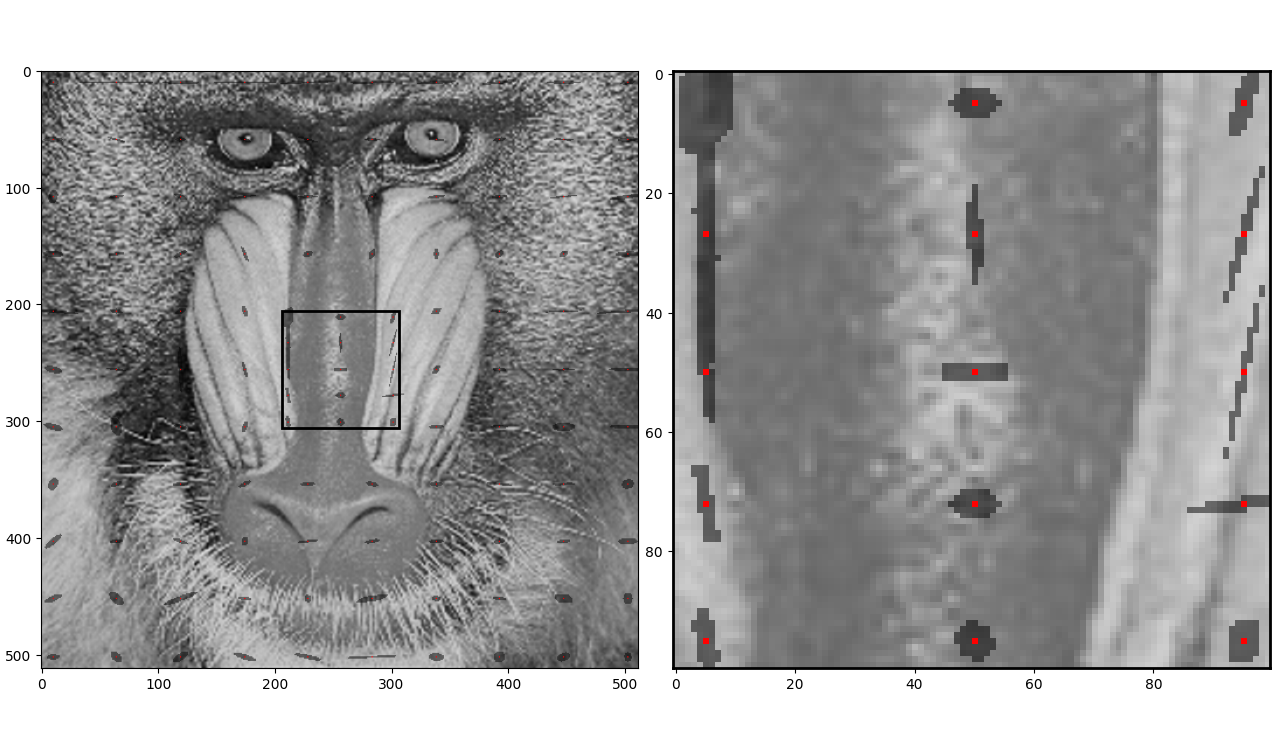
In my research, I incorporate geometric principles into the analysis of functionals arising in statistics and machine learning.
Key Research Themes:
- Making ML algorithms more computationally and statistically efficient.
- Leveraging geometric structure in data.
- Re-imagining classical methods in modern settings.
To tackle these problems, I use tools from functional analysis, entropic optimal transport, numerical linear algebra, and empirical processes.